| Quick Access to my selection Last Update: 2022-10-24 09:36:42 Ireland Time / 2022-10-24 01:36:42 PDT-0700 Unix epoch: 1666600602 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Installing PHP environment for development in Windows
This article is for my students learning PHP, or for any student that wants to learn PHP and uses a Windows computer for that.
For this we will install:
XAMPP, which is available for Windows, Mac OS and Linux.
You can download it from: https://www.apachefriends.org/
XAMPP installs together:
- Apache
- MariaDB
- PHP
- Perl
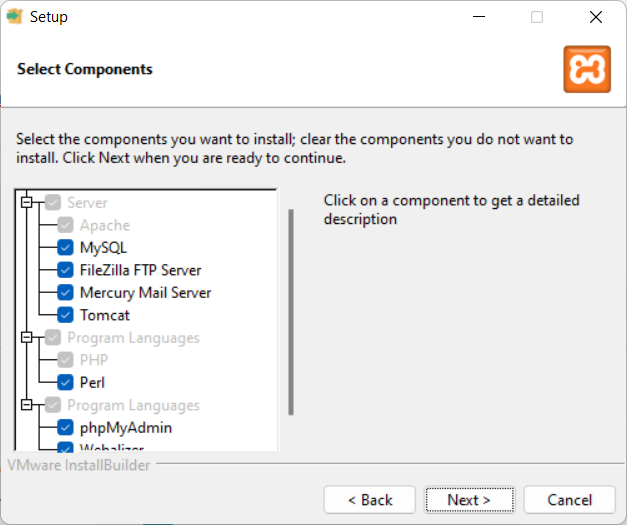
Install WAMPP instead of XAMP (if you prefer WAMPP)
Alternatively you can install WAMPP, which installs:
- Apache
- MySQL
- PHP
- PHPMyAdmin
https://www.wampserver.com/en/

Development IDE
As Development Environment we will use PHPStorm, from Jetbrains.
https://www.jetbrains.com/phpstorm/
Testing the installation of XAMPP
The default directory for the PHP files is C:\xampp\htdocs
Create a file in c:\xampp\htdocs named hello.php
<?php
$s_today = date("Y-m-d");
echo "Hello! Today is ".$s_today;
?>
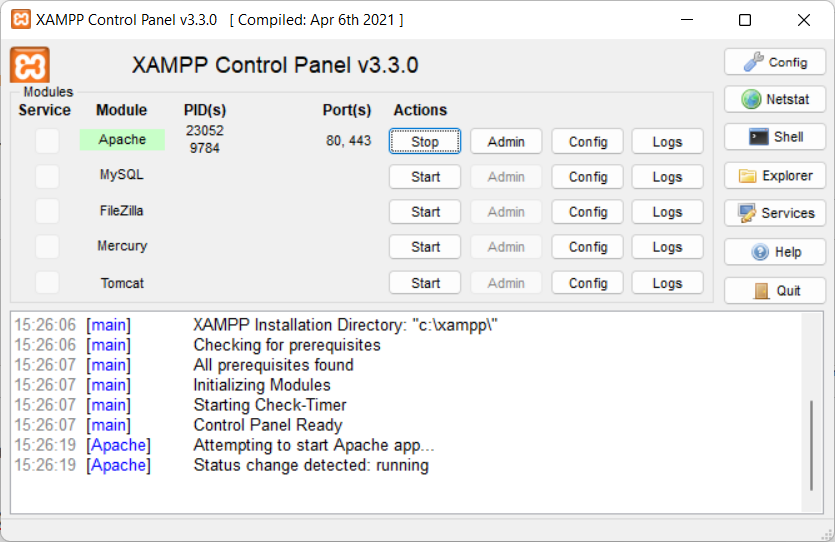
Now start Apache:
- Open the XAMPP Control Panel
- Start the Apache Server
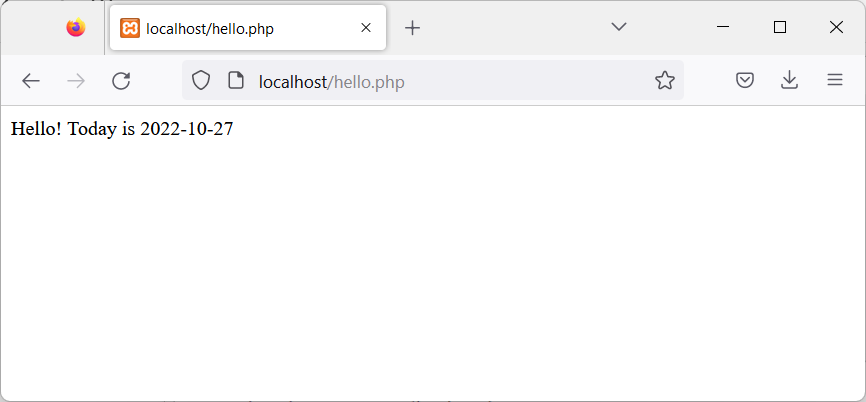
And test the new page, with the browser, opening:
http://localhost/hello.php
Backup and Restore your Ubuntu Linux Workstations
This is a mechanism I invented and I’ve been using for decades, to migrate or clone my Linux Desktops to other physical servers.
This script is focused on doing the job for Ubuntu but I was doing this already 30 years ago, for X Window as I was responsible of the Linux platform of a ISP (Internet Service Provider). So, it is compatible with any Linux Desktop or Server.
It has the advantage that is a very lightweight backup. You don’t need to backup /etc or /var as long as you install a new OS and restore the folders that you did backup. You can backup and restore Wine (Windows Emulator) programs completely and to/from VMs and Instances as well.
It’s based on user/s rather than machine.
And it does backup using the Timestamp, so you keep all the different version, modified over time. You can fusion the backups in the same folder if you prefer avoiding time versions and keep only the latest backup. If that’s your case, then replace s_PATH_BACKUP_NOW=”${s_PATH_BACKUP}${s_DATETIME}/” by s_PATH_BACKUP_NOW=”${s_PATH_BACKUP}” for instance. You can also add a folder for machine if you prefer it, for example if you use the same userid across several Desktops/Servers.
I offer you a much simplified version of my scripts, but they can highly serve your needs.
#!/usr/bin/env bash
# Author: Carles Mateo
# Last Update: 2022-10-23 10:48 Irish Time
# User we want to backup data for
s_USER="carles"
# Target PATH for the Backups
s_PATH_BACKUP="/home/${s_USER}/Desktop/Bck/"
s_DATE=$(date +"%Y-%m-%d")
s_DATETIME=$(date +"%Y-%m-%d-%H-%M-%S")
s_PATH_BACKUP_NOW="${s_PATH_BACKUP}${s_DATETIME}/"
echo "Creating path $s_PATH_BACKUP and $s_PATH_BACKUP_NOW"
mkdir $s_PATH_BACKUP
mkdir $s_PATH_BACKUP_NOW
s_PATH_KEY="/home/${s_USER}/Desktop/keys/2007-01-07-cloud23.pem"
s_DOCKER_IMG_JENKINS_EXPORT=${s_DATE}-jenkins-base.tar
s_DOCKER_IMG_JENKINS_BLUEOCEAN2_EXPORT=${s_DATE}-jenkins-blueocean2.tar
s_PGP_FILE=${s_DATETIME}-pgp.zip
# Version the PGP files
echo "Compressing the PGP files as ${s_PGP_FILE}"
zip -r ${s_PATH_BACKUP_NOW}${s_PGP_FILE} /home/${s_USER}/Desktop/PGP/*
# Copy to BCK folder, or ZFS or to an external drive Locally as defined in: s_PATH_BACKUP_NOW
echo "Copying Data to ${s_PATH_BACKUP_NOW}/Data"
rsync -a --exclude={} --acls --xattrs --owner --group --times --stats --human-readable --progress -z "/home/${s_USER}/Desktop/data/" "${s_PATH_BACKUP_NOW}data/"
rsync -a --exclude={'Desktop','Downloads','.local/share/Trash/','.local/lib/python2.7/','.local/lib/python3.6/','.local/lib/python3.8/','.local/lib/python3.10/','.cache/JetBrains/'} --acls --xattrs --owner --group --times --stats --human-readable --progress -z "/home/${s_USER}/" "${s_PATH_BACKUP_NOW}home/${s_USER}/"
rsync -a --exclude={} --acls --xattrs --owner --group --times --stats --human-readable --progress -z "/home/${s_USER}/Desktop/code/" "${s_PATH_BACKUP_NOW}code/"
echo "Showing backup dir ${s_PATH_BACKUP_NOW}"
ls -hal ${s_PATH_BACKUP_NOW}
df -h /
See how I exclude certain folders like the Desktop or Downloads with –exclude.
It relies on the very useful rsync program. It also relies on zip to compress entire folders (PGP Keys on the example).
If you use the second part, to compress Docker Images (Jenkins in this example), you will run it as sudo and you will need also gzip.
# continuation... sudo running required.
# Save Docker Images
echo "Saving Docker Jenkins /home/${s_USER}/Desktop/Docker_Images/${s_DOCKER_IMG_JENKINS_EXPORT}"
sudo docker save jenkins:base --output /home/${s_USER}/Desktop/Docker_Images/${s_DOCKER_IMG_JENKINS_EXPORT}
echo "Saving Docker Jenkins /home/${s_USER}/Desktop/Docker_Images/${s_DOCKER_IMG_JENKINS_BLUEOCEAN2_EXPORT}"
sudo docker save jenkins:base --output /home/${s_USER}/Desktop/Docker_Images/${s_DOCKER_IMG_JENKINS_BLUEOCEAN2_EXPORT}
echo "Setting permissions"
sudo chown ${s_USER}.${s_USER} /home/${s_USER}/Desktop/Docker_Images/${s_DOCKER_IMG_JENKINS_EXPORT}
sudo chown ${s_USER}.${s_USER} /home/${s_USER}/Desktop/Docker_Images/${s_DOCKER_IMG_JENKINS_BLUEOCEAN2_EXPORT}
echo "Compressing /home/${s_USER}/Desktop/Docker_Images/${s_DOCKER_IMG_JENKINS_EXPORT}"
gzip /home/${s_USER}/Desktop/Docker_Images/${s_DOCKER_IMG_JENKINS_EXPORT}
gzip /home/${s_USER}/Desktop/Docker_Images/${s_DOCKER_IMG_JENKINS_BLUEOCEAN2_EXPORT}
rsync -a --exclude={} --acls --xattrs --owner --group --times --stats --human-readable --progress -z "/home/${s_USER}/Desktop/Docker_Images/" "${s_PATH_BACKUP_NOW}Docker_Images/"
There is a final part, if you want to backup to a remote Server/s using ssh:
# continuation... to copy to a remote Server.
s_PATH_REMOTE="bck7@cloubbck11.carlesmateo.com:/Bck/Desktop/${s_USER}/data/"
# Copy to the other Server
rsync -e "ssh -i $s_PATH_KEY" -a --exclude={} --acls --xattrs --owner --group --times --stats --human-readable --progress -z "/home/${s_USER}/Desktop/data/" ${s_PATH_REMOTE}
I recommend you to use the same methodology in all your Desktops, like for example, having a data/ folder in the Desktop for each user.
You can use Erasure Code to split the Backups in blocks and store a piece in different Cloud Providers.
Also you can store your Backups long-term, with services like Amazon Glacier.
Other ideas are storing certain files in git and in Hadoop HDFS.
If you want you can CRC your files before copying to another device or server.
You will use tools like: sha512sum or md5sum.
CTOP.py video on the Activision Blizzard King IT Demos 2021 February
I’ve good memories of this video.
In the middle of pandemic, with all commerce’s closed and no access to better cameras or equipment, I demonstrated the plug-in architecture that I created and I added to my CTOP.py Open Source Python Monitoring tool in a global conference for all IT in ABK (Activision Blizzard King).
I was so proud.
For that I cloned ctop into a Raspberry Pi 4 with Ubuntu LTS and had that motherboard which is a Christmas Tree LED attached to the GPIO.
As the CPU load on the Raspberry was low, the LED’s were green, and a voice (recorded and provided by an Irish friend) was played “The System is Healthy”.
Then I added load to the CPU and the LED’s changed.
And I added more load to the CPU and the LED’s turned to Red and and human voice “CPU load is too high”.
Voice is only played after a change in the state and with a cool down of a minute, to prevent flapping situations to keep the program chatting like a parrot :)
I should have shaved myself, but you know, it was a savage pandemic.
Also a manager from Blizzard DM me and told me that the touch pad being emerged was due to the battery swallowing and that it could explode, so I requested a replacement. Then I explained to other colleagues with the same symptom, and to others with no problems so they are not at risk if the same happened to them.
WFH made things that would be quickly detected in the offices by others (like the touchpad emerging) go unnoticed.
if you are looking for source code, it is in the CTOP’s gitlab repository. However it’s advanced Python plugin architecture code.
If you just look for a sample of how to power on the LED’s in different colors, and the tricks for solving any problem you may encounter, then look at it here:
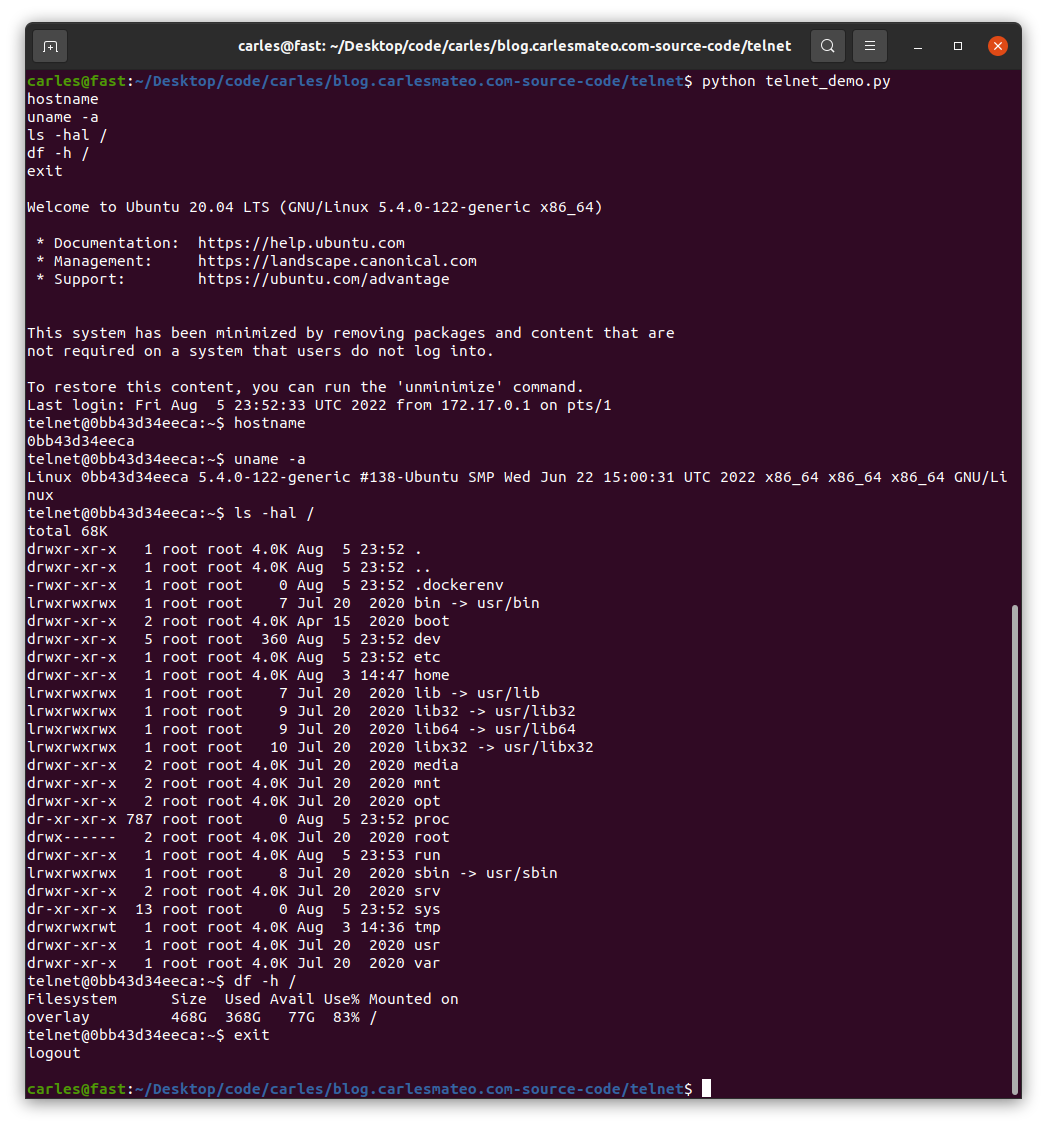
Docker with Ubuntu with telnet server and Python code to access via telnet
Here you can see this Python code to connect via Telnet and executing a command in a Server:
File: telnet_demo.py
#!/usr/bin/env python3
import telnetlib
s_host = "localhost"
s_user = "telnet"
s_password = "telnet"
o_tn = telnetlib.Telnet(s_host)
o_tn.read_until(b"login: ")
o_tn.write(s_user.encode('ascii') + b"\n")
o_tn.read_until(b"Password: ")
o_tn.write(s_password.encode('ascii') + b"\n")
o_tn.write(b"hostname\n")
o_tn.write(b"uname -a\n")
o_tn.write(b"ls -hal /\n")
o_tn.write(b"exit\n")
print(o_tn.read_all().decode('ascii'))
File: Dockerfile
FROM ubuntu:20.04 MAINTAINER Carles Mateo ARG DEBIAN_FRONTEND=noninteractive # This will make sure printing in the Screen when running in detached mode ENV PYTHONUNBUFFERED=1 RUN apt-get update -y && apt install -y sudo telnetd vim systemctl && apt-get clean RUN adduser -gecos --disabled-password --shell /bin/bash telnet RUN echo "telnet:telnet" | chpasswd EXPOSE 23 CMD systemctl start inetd; while [ true ]; do sleep 60; done
You can see that I use chpasswd command to change the password for the user telnet and set it to telnet. That deals with the complexity of setting the encrypted password.
File: build_docker.sh
#!/bin/bash
s_DOCKER_IMAGE_NAME="ubuntu_telnet"
echo "We will build the Docker Image and name it: ${s_DOCKER_IMAGE_NAME}"
echo "After, we will be able to run a Docker Container based on it."
printf "Removing old image %s\n" "${s_DOCKER_IMAGE_NAME}"
sudo docker rm "${s_DOCKER_IMAGE_NAME}"
printf "Creating Docker Image %s\n" "${s_DOCKER_IMAGE_NAME}"
sudo docker build -t ${s_DOCKER_IMAGE_NAME} .
# If you don't want to use cache this is your line
# sudo docker build -t ${s_DOCKER_IMAGE_NAME} . --no-cache
i_EXIT_CODE=$?
if [ $i_EXIT_CODE -ne 0 ]; then
printf "Error. Exit code %s\n" ${i_EXIT_CODE}
exit
fi
echo "Ready to run ${s_DOCKER_IMAGE_NAME} Docker Container"
echo "To run in type: sudo docker run -it -p 23:23 --name ${s_DOCKER_IMAGE_NAME} ${s_DOCKER_IMAGE_NAME}"
When you run sudo ./build_docker.sh the image will be built. Then run it with:
sudo docker run -it -p 23:23 --name ubuntu_telnet ubuntu_telnet
If you get an error indicating that the port is in use, then your computer has already a process listening on the port 23, use another.
You will be able to stop the Container by pressing CTRL + C
From another terminal run the Python program:
python3 ./telnet_demo.py
Validate IP Addresses and Networks with CIDR in Python
Python has a built-in package named ipaddress
You don’t need to install anything to use it.
This simple code shows how to use it
import ipaddress
def check_ip(s_ip_or_net):
b_valid = True
try:
# The IP Addresses are expected to be passed without / even if it's /32 it would fail
# If it uses / so, the CIDR notation, check it as a Network, even if it's /32
if "/" in s_ip_or_net:
o_net = ipaddress.ip_network(s_ip_or_net)
else:
o_ip = ipaddress.ip_address(s_ip_or_net)
except ValueError:
b_valid = False
return b_valid
if __name__ == "__main__":
a_ips = ["127.0.0.2.4",
"127.0.0.0",
"192.168.0.0",
"192.168.0.1",
"192.168.0.1 ",
"192.168.0. 1",
"192.168.0.1/32",
"192.168.0.1 /32",
"192.168.0.0/32",
"192.0.2.0/255.255.255.0",
"0.0.0.0/31",
"0.0.0.0/32",
"0.0.0.0/33",
"1.2.3.4",
"1.2.3.4/24",
"1.2.3.0/24"]
for s_ip in a_ips:
b_success = check_ip(s_ip)
if b_success is True:
print(f"The IP Address or Network {s_ip} is valid")
else:
print(f"The IP Address or Network {s_ip} is not valid")
And the output is like this:
The IP Address or Network 127.0.0.2.4 is not valid The IP Address or Network 127.0.0.0 is valid The IP Address or Network 192.168.0.0 is valid The IP Address or Network 192.168.0.1 is valid The IP Address or Network 192.168.0.1 is not valid The IP Address or Network 192.168.0. 1 is not valid The IP Address or Network 192.168.0.1/32 is valid The IP Address or Network 192.168.0.1 /32 is not valid The IP Address or Network 192.168.0.0/32 is valid The IP Address or Network 192.0.2.0/255.255.255.0 is valid The IP Address or Network 0.0.0.0/31 is valid The IP Address or Network 0.0.0.0/32 is valid The IP Address or Network 0.0.0.0/33 is not valid The IP Address or Network 1.2.3.4 is valid The IP Address or Network 1.2.3.4/24 is not valid The IP Address or Network 1.2.3.0/24 is valid
As you can read in the code comments, ipaddress.ip_address() will not validate an IP Address with the CIDR notation, even if it’s /32.
You should strip the /32 or use ipaddress.ip_network() instead.
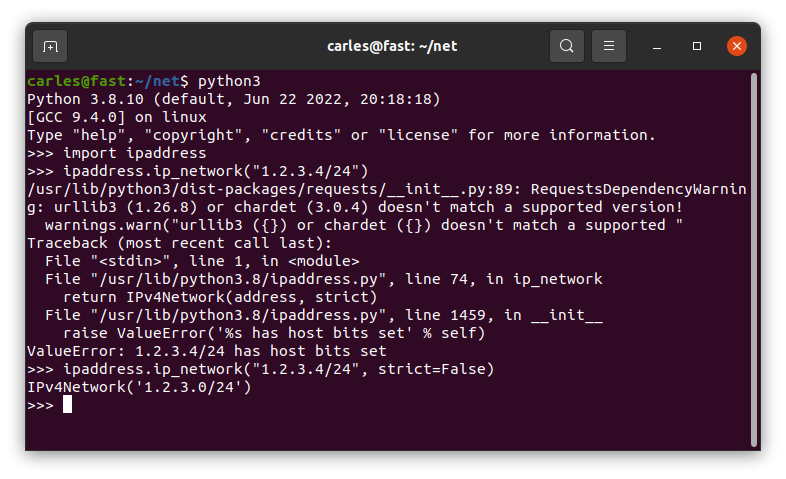
As you can see 1.2.3.4/24 is returned as not valid.
You can pass the parameter strict=False and it will be returned as valid.
ipaddress.ip_network(s_ip_or_net, strict=False)
See where is the space used in your Android phone from Ubuntu Terminal
So, you may have your Android phone full and you don’t know where the space is.
You may have tried Apps for Android but none shows the information in the detail you would like. Linux to the rescue.
First of all you need a cable able to transfer Data. It is a cable that will be connected to your computer, normally with an USB 3.0 cable and to your smartphone, normally with USB-C.
Sometimes phone’s connectors are dirty and don’t allow a stable connection. Your connections should allow a stable connection, otherwise the connection will be interrupted in the middle.
Once you connect the Android smartphone to the computer, unlock the phone and authorize the data connection.
You’ll see that your computer recognizes the phone:
Open the terminal and enter this directory:
cd /run/user/1000/gvfs/
Here you will see your device and the name is very evident.
The usual is to have just one device listed, but if you had several Android devices attached you may want to query first, in order to identify it.
The Android devices use a protocol named Media Transfer Protocol (MTP) when connecting to the USB port, and that’s different on the typical way to access the USB port.
usb-devices | grep "Manufacturer=" -B 3
Run this command to see all the devices connected to the USB.
You may see Manufacturer=SAMSUNG or Manufacturer=OnePlus etc…
The information returned will allow you to identify your device in /run/user/1000/gvfs/
You may get different type of outputs, but if you get:
T: Bus=02 Lev=01 Prnt=01 Port=00 Cnt=01 Dev#= 13 Spd=480 MxCh= 0
your device can be accessed inside:
cd mtp\:host\=%5Busb%3A002%2C013%5D/
There you’ll see Card and Phone.
You can enter the Phone internal storage or the SD Card storage directory:
cd Phone
To see how the space is distributed nicely I recommend you to use the program ncdu if you don’t have you can install it with:
sudo apt install ncdu
Then run ncdu:
ncdu
It will calculate the space…
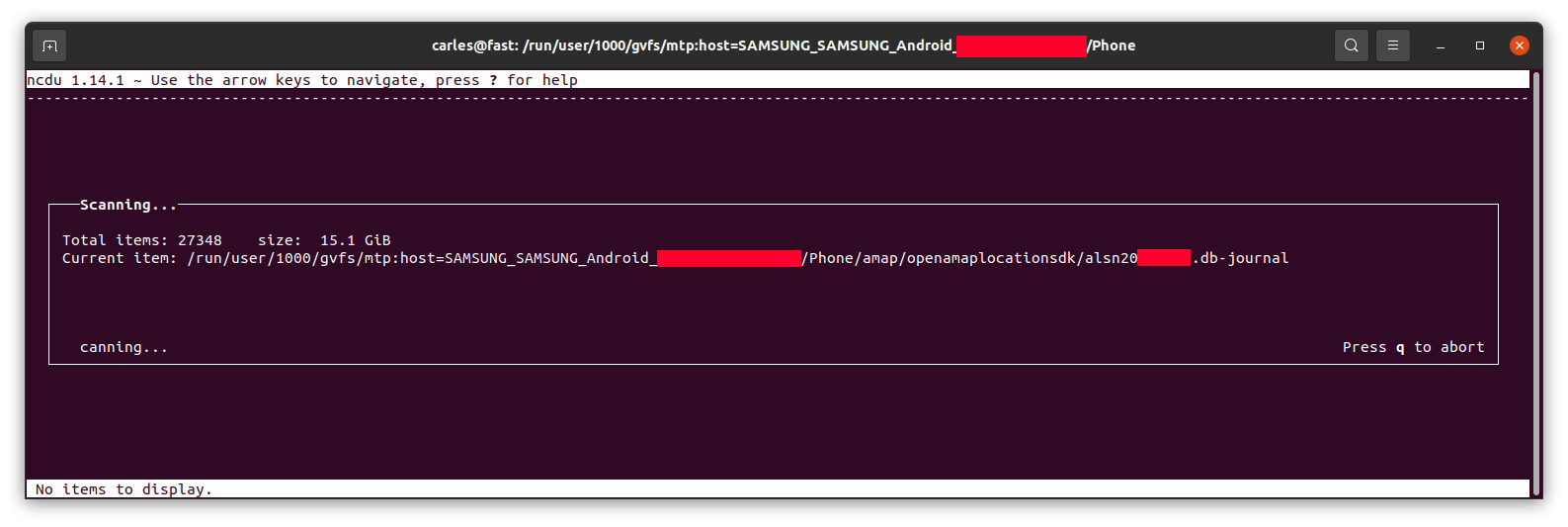
… and let you know, sorted from more to less, and will allow you to browse the sub-directories with the keyboard arrow keys and enter to get major clarity.
For example, in my case I saw 8.5 GB in the folder Movies on the phone, where I didn’t download any movie, so I checked.
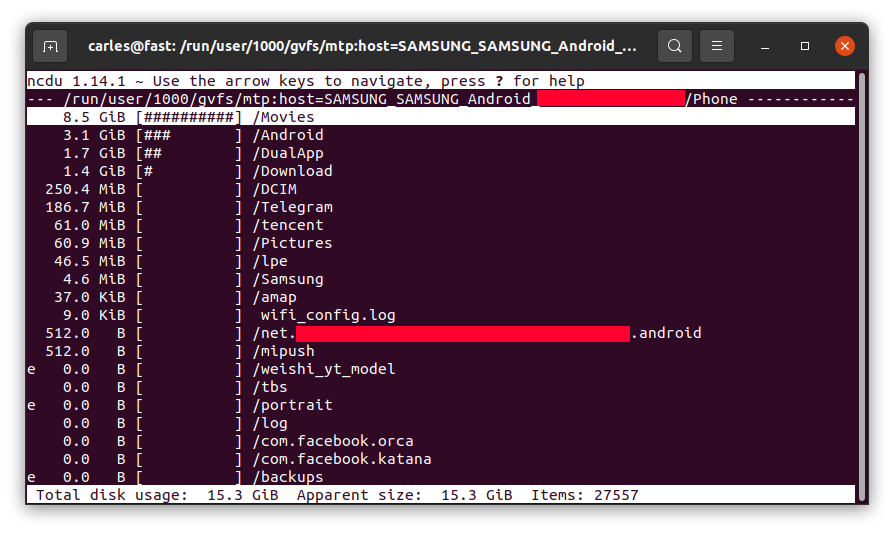
I entered inside by pressing Enter:
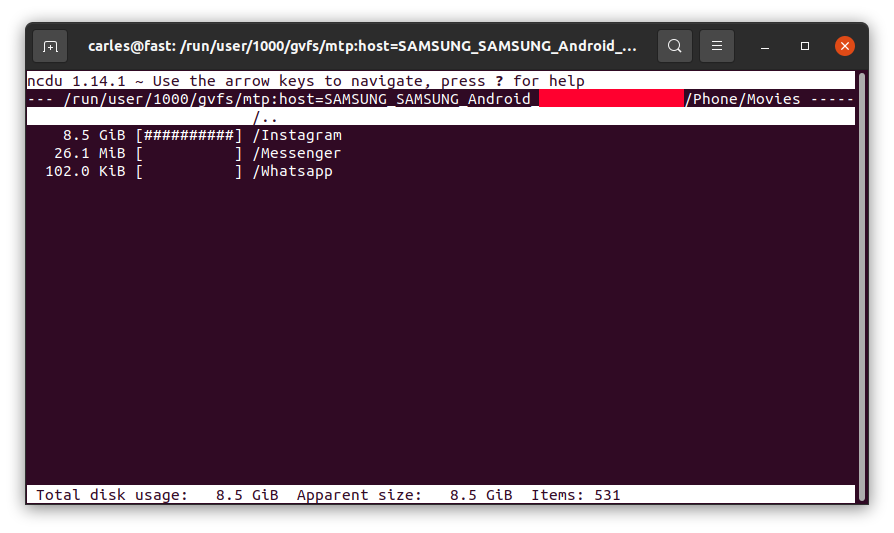
So Instagram App was keeping a copy all the videos I uploaded, in total 8.5 GB of my Phone’s space and never releasing them!.
Example for the SD card, where the usage was as expected:
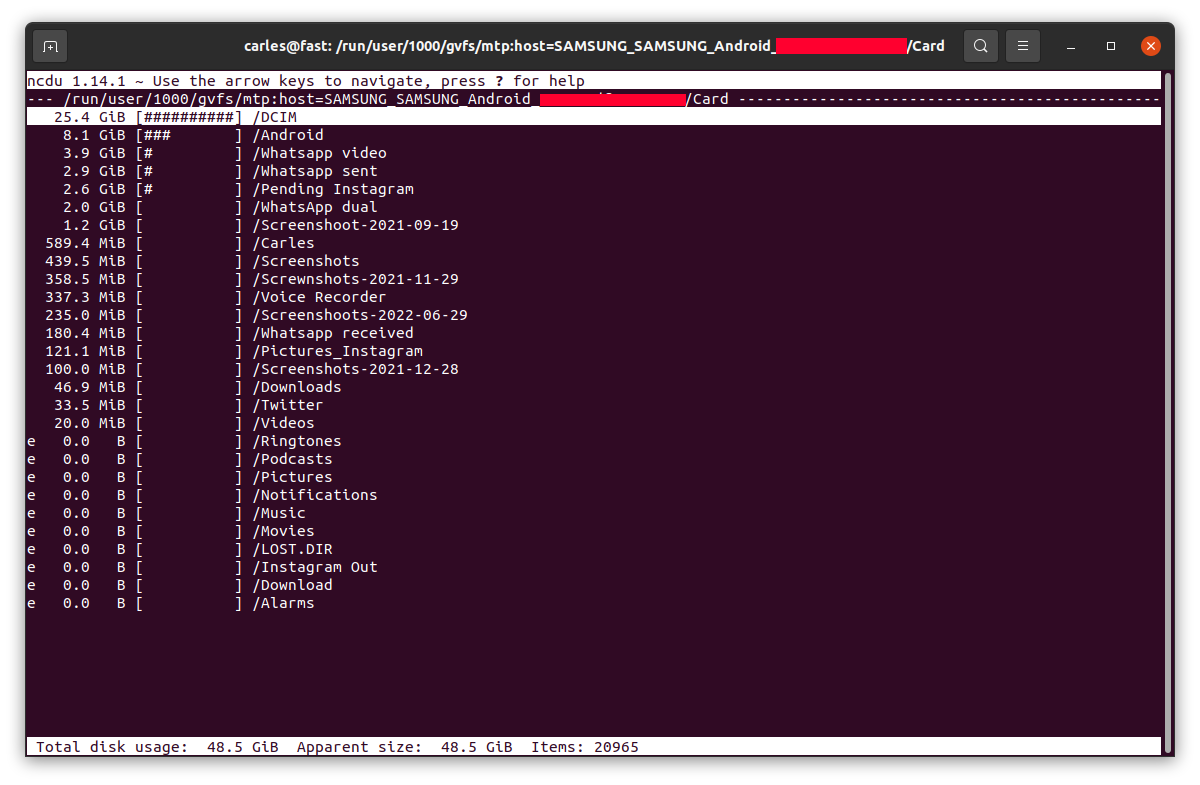
News from the blog 2022-07-22
Carles in the News
For all my friends and followers, I started to translate my radio space “El nou món digital” (in Catalan) to English “The New Digital World”. I cover Science, Technology, Entertainment and Video games.
You can see the first programs I translated here:
Catalan and English programs RAB
And the script and links mentioned here:
https://blog.carlesmateo.com/2022/06/20/rab-el-nou-mon-digital-2022-06-27-ca/
Social
I’ve created an Instagram fan page for me / for the blog.
It is open for everybody.
https://www.instagram.com/blog_carlesmateo/
Videos for learning how to code
Learning How to code Python Unit Tests with pytest from the scratch, for beginners:
I added it to my series of videos:
https://blog.carlesmateo.com/learn-python-3-unit-testing/
Video for learning how to use RabbitMQ with Python in a Docker Container
Site carlesmateo.com
I use mostly this site https://blog.carlesmateo.com to centralize everything, so I’ve kept http://carlesmateo.com as a simple landing page made with my old (from 2013) ultra fast PHP Framework Catalonia Framework.
I decided to create a Jenkins Pipeline to deploy any updates to this pages and I updated it a bit at least to provide the most common information searched.
Don’t expect anything fancy at Front End level. :)
Cloud
I created a video about how to provision a Ubuntu Droplet in Digital Ocean.
It’s just for beginners, or if you used other CSP’s and you wonder how Digital Ocean user interface is.
It is really easy, to be honest. Amazon AWS should learn from them.
I also created another about how to provision using User Data Cloud Init feature:
Books
My Books
I have updated Docker Combat Guide to show how to work with different users in the Dockerfile and accessing an interactive terminal.
I have also added how to create a Jenkins containerized.
Books I bought > CI/CD
I recommend you these books:

I’ve created a video about how to deploy jenkins in Docker, following the official documentation, in 4 minutes.
Install jenkins on Docker in ubuntu in 4 minutes
And posted an article about solving the error load key invalid format when provisioning from Jenkins with your SSH .pem Key in a variable.
Open Source from Carles
CTOP.py
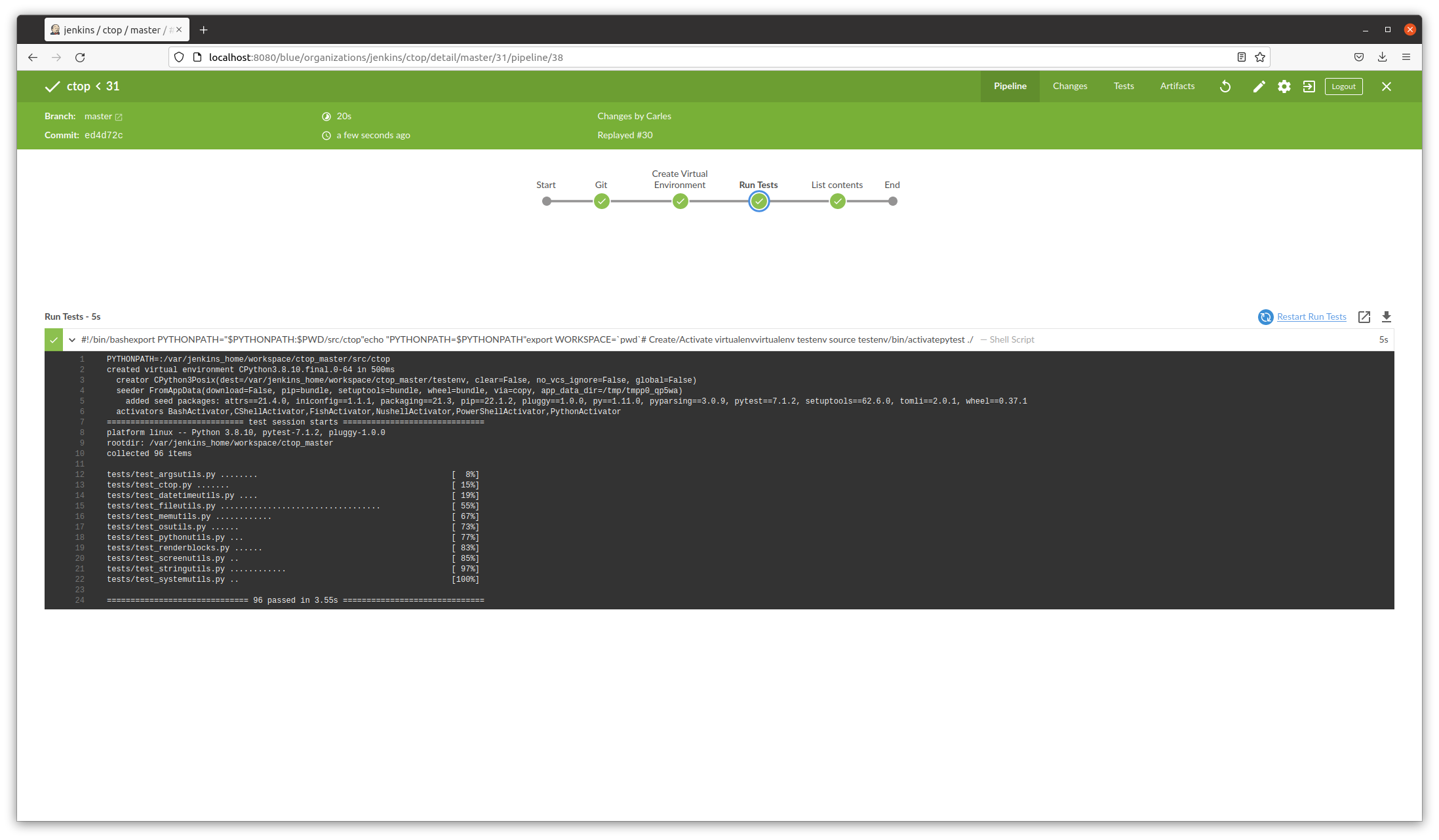
I have released a new version of CTOP, ctop.py version 0.8.9.
This version fixes few bugs, and adds better Unit Testing Code Coverage, and is integrated with jenkins (provides Jenkinsfile and a Dockerfile ready to automate the testing pipeline)
Sudo ku solver, Sudoku solver in Python, and Engineering solving problem approach
I’ve created this video explaining my experience writing a program to solve two impossible, very annoying Sudokus. :)
https://blog.carlesmateo.com/2022/04/26/working-on-a-sudoku-solver-in-python-source-code/
Commander Turtle: a small program in Python so children can learn to code by drawing
Children can learn to code and share their scripts, which are comma separated, easily.
My life at Activision Blizzard
We have released World of Warcraft Dragonflight Alpha.
In the sync meetings I lead with Wow SRE and product Team I was informed that streaming would be open. Myself I was granted to stream over twitch, but so far I didn’t want to stream video games in my engineering channels. It’s different kind of audiences IMO. Let me know if you would like to get video game streams in my streaming channels.

Humor



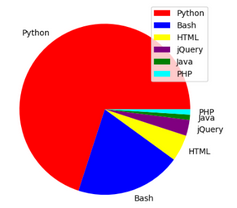
Video: Parse the Tables from a Website with Python pandas
A quick video, of 3 minutes, that shows you how it works.
If you don’t have pandas installed you’ll have to install it and lxml, otherwise you’ll get an error:
File "/home/carles/Desktop/code/carles/blog.carlesmateo.com-source-code/venv/lib/python3.8/site-packages/pandas/io/html.py", line 872, in _parser_dispatch
raise ImportError("lxml not found, please install it")
ImportError: lxml not found, please install it
You can install both from PyCharm or from command line with:
pip install pandas pip install lxml
And here the source code:
import pandas as pd
if __name__ == "__main__":
# Do not truncate the data when printing
pd.set_option('display.max_colwidth', None)
# Do not truncate due to length of all the columns
pd.set_option('display.max_columns', None)
pd.set_option('display.max_rows', None)
pd.set_option('display.width', 2000)
# pd.set_option('display.float_format', '{:20,.2f}'.format)
o_pd_my_movies = pd.read_html("https://blog.carlesmateo.com/movies-i-saw/")
print(len(o_pd_my_movies))
print(o_pd_my_movies[0])
Video: How to create a Docker Container for LAMPP step by step
How to create a Docker Container for Linux Apache MySQL PHP and Python for beginners.
Note: Containers are not persistent. Use this for tests only. If you want to keep persistent information use Volumes.
File: Dockerfile
FROM ubuntu:20.04
MAINTAINER Carles Mateo
ARG DEBIAN_FRONTEND=noninteractive
RUN apt update && \
apt install -y vim python3-pip && \
apt install -y net-tools mc vim htop less strace zip gzip lynx && \
apt install -y apache2 mysql-server ntpdate libapache2-mod-php7.4 mysql-server php7.4-mysql php-dev libmcrypt-dev php-pear && \
apt install -y git && apt autoremove && apt clean && \
pip3 install pytest
RUN a2enmod rewrite
RUN echo "Europe/Ireland" | tee /etc/timezone
ENV APACHE_RUN_USER www-data
ENV APACHE_RUN_GROUP www-data
ENV APACHE_LOG_DIR /var/log/apache2
ENV APACHE_PID_FILE /var/run/apache2/apache2.pid
ENV APACHE_RUN_DIR /var/run/apache2
ENV APACHE_LOCK_DIR /var/lock/apache2
ENV APACHE_LOG_DIR /var/log/apache2
COPY phpinfo.php /var/www/html/
RUN service apache2 restart
EXPOSE 80
CMD ["/usr/sbin/apache2", "-D", "FOREGROUND"]
File: phpinfo.php
<html> <?php // Show all information, defaults to INFO_ALL phpinfo(); // Show just the module information. // phpinfo(8) yields identical results. phpinfo(INFO_MODULES); ?> </html>
File: build_docker.sh
#!/bin/bash
s_DOCKER_IMAGE_NAME="lampp"
echo "We will build the Docker Image and name it: ${s_DOCKER_IMAGE_NAME}"
echo "After, we will be able to run a Docker Container based on it."
printf "Removing old image %s\n" "${s_DOCKER_IMAGE_NAME}"
sudo docker rm "${s_DOCKER_IMAGE_NAME}"
printf "Creating Docker Image %s\n" "${s_DOCKER_IMAGE_NAME}"
# sudo docker build -t ${s_DOCKER_IMAGE_NAME} . --no-cache
sudo docker build -t ${s_DOCKER_IMAGE_NAME} .
i_EXIT_CODE=$?
if [ $i_EXIT_CODE -ne 0 ]; then
printf "Error. Exit code %s\n" ${i_EXIT_CODE}
exit
fi
echo "Ready to run ${s_DOCKER_IMAGE_NAME} Docker Container"
echo "To run in type: sudo docker run -p 80:80 --name ${s_DOCKER_IMAGE_NAME} ${s_DOCKER_IMAGE_NAME}"
echo "or just use run_in_docker.sh"
echo
echo "If you want to debug do:"
echo "docker exec -i -t ${s_DOCKER_IMAGE_NAME} /bin/bash"